How to Draw Mohr’s Circle

Mohr’s Circle is used to graphically determine the principal normal and shear stresses.

First, some definitions:

• Tensile stresses are positive.
• Compressive stresses are negative.
• Clockwise shear stresses are positive.
• Counterclockwise shear stresses are negative.

To draw Mohr’s circle, and find the principal normal and shear stresses, you must know the stresses applied to the object, σ_x, σ_y, τ_xy.

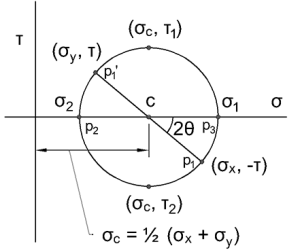
1. Draw a set of σ-τ axes
2. Using the following formula, locate the center of the circle, point c.
   $latex \sigma_{c} = \frac{1}{2}(\sigma_{x} + \sigma_{y})$
3. Using the following formula, locate the point p₁
   $latex p_{1} = (\sigma_{x}, -\tau_{xy})$
4. Using point c as the center, and p₁ on the circle, draw the rest of the circle.
5. Draw a line straight across the circle from point p₁, through the center c, and to the other opposite point. Call this point p’₁.
6. The point at which the circle overlaps the σ axis are points p₂ and p₃, the smaller and larger principle stresses, respectively.
7. Determine the angle θ, which is half of the angle 2θ on the circle.
8. The top and bottom of the circle are the largest and smallest shear stresses, respectively.