Bernoulli Equation Examples

October 11, 2013 by Leave a Comment

For reference, the Bernoulli equation is:

E_t = E_p + E_v + E_z\newline \indent =\frac{p}{\rho}+\frac{v^{2}}{2}+zg\hspace{20px}^{(SI)}\newline \indent =\frac{p}{\rho}+\frac{v^{2}}{2g_c}+\frac{zg}{g_c}\hspace{20px}^{(US)}

Example 1

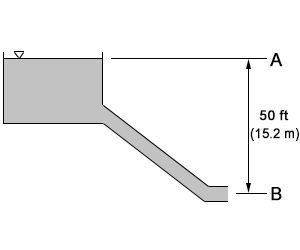
A reservoir contains an outlet that consists of a pipe that discharges water 50 ft below the top of the reservoir.

What is the velocity of the water exiting the pipe (at point B)?

Solution

If you define elevation zero at point B:

  • Point A has only potential energy
  • Point B has only kinetic energy

The Bernoulli equation states that total energy must be the same, therefore:

U.S. Units Metric
E_{tA} = E_{tB}\newline\newline 0 + 0 + \frac{z_A g}{g_c} = 0 + \frac{v_B^{2}}{2g_c} + 0\newline\newline\frac{(50 ft)(32.2 ft/s^{2})}{32.2 \frac{lbm\cdot ft}{lbf\cdot s^{2}}} = \frac{v^{2}}{2(32.2 \frac{lbm\cdot ft}{lbf\cdot s^{2}})}\newline\newline\newline v = 56.7 ft/s E_{tA} = E_{tB}\newline\newline 0 + 0 + z_A g = 0 + \frac{v_B^{2}}{2} + 0\newline\newline (15.2 m)(9.81 m/s^{2}) = \frac{v^{2}}{2}\newline\newline\newline v = 17.3 m/s

 

Example 2

A pump is pumping water up a hillside into a reservoir. The pump rate is 4 ft/s (1.22 m/s) with a pressure of 100 psi (689 kPa). What is the maximum elevation of the reservoir that the pump can handle? (Water = 62.4 lbm/ft3 or 1000 kg/m3).

Solution

  • The pump has both pressure and kinetic energy
  • The reservoir has only potential energy

According to Bernoulli’s principle, the sum of the energy must be the same at both locations.

U.S. Units Metric
E_{t\cdot pump} = E_{t\cdot reservoir}\newline\newline \frac{p}{\rho} + \frac{v^{2}}{2g_c} + 0 = 0 + 0 + zg_c\newline\newline \frac{100 psi}{62.4 lbm/ft^{3}} + \frac{(4 ft/s)^{2}}{2(32.2 \frac{lbm\cdot ft}{lbf\cdot s^{2}})}= \newline\newline \hspace{50px}= \frac{z\cdot (32.2 ft/s^{2})}{32.2 \frac{lbm \cdot ft}{lbf\cdot s^{2}}}\newline\newline\newline z = 231.0 ft E_{t\cdot pump} = E_{t\cdot reservoir}\newline\newline \frac{p}{\rho} + \frac{v^{2}}{2} + 0 = 0 + 0 + zg\newline\newline \frac{689 kPa}{1000kg/m^{3}} + \frac{(1.22 m/s)^{2}}{2}= \newline\newline\hspace{50px}= z\cdot (9.81 m/s^{2})\newline\newline\newline z = 70.3 m
Filed Under: Uncategorized Tagged With: , , , , , ,

Speak Your Mind

*

This site uses Akismet to reduce spam. Learn how your comment data is processed.